ここでは正弦波のみを考える。周波数440Hzの音を、 A4(ラ)と名づける。その倍の周波数を持つ音(880Hz)はA5、さらに1760HzはA6、のように名づけていこう。
A3からA4の間の区間は1オクターブである。1オクターブから12の音を選ぶ。 なぜ12なのか、は私には分からないが、西洋音楽とはそういうものらしい。 選び方は、周波数が等比数列となるようにする。公比は 2^(1/12)である。 この選び方によって、A3からA4の間には、 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 の音が存在する。A3とA4は、0と12にそれぞれ対応する。1オクターブは {0,1,2,...,11} という集合で現される。A4からA5の間などにも同様に拡張すると、結局 ある特定の周波数の音に、整数でラベルをつけることができる。
実際MIDIのノートナンバーは、上のように整数で名前がつけられている。たとえばA4の音(440Hz)は69である。当然、A5の音(880Hz)は、69+12=81となる。
音楽理論では、1オクターブ離れた音は同じものとみなすようだ。 よって、 0 ~= 12 であり、3~=15 である。 つまり、12で割った余りで作る剰余類を考えることになる。
440Hzの音を0とするとき、
{0,2,3,5,7,8,10}
に対応する音に
{A,B,C,D,E,F,G}
と名づける。(日本語だとイロハニホヘトを使う。本サイトではなるべく数字表記で統一し、英字表記を併用する)
さて、これは音名であり、周波数を指定する。
アルファベットは、音名にも音階にも使われて大混乱だが、音名は周波数を指定する。
絶対音名とでも名づければよかろうか。
いきなり仲間外れにされてしまった
{1,4,6,9,11}
の5個には
{A#, C#, D#, F#,G#}
というやや強引な名前が付いている。
これらの音はあまり使われない、というわけでは決してない。
国際表記では、オクターブ表記の方法として A3,B3,C4,D4,E4,F4,G4,A4,B4,C5,D5 のように表記するらしい。つまり、CからBまでを1オクターブの区切りとしている。 なんでそんなことになっているのかは、下のドレミと関係しそうだが、何にせよ複雑なことになっている、という感はぬぐえない。
半音の差とは、差が1であること 全音の差とは、差が2であること 間隔が1度とは、間隔がないこと(すごい定義です・・・) 間隔が3度とは、間隔が+4または+3のこと(それぞれ、長3度と短3度というらしい) 間隔が完全5度とは、間隔が+7のこと。 完全5度の差は、周波数の比が2^(7/12)=1.498..となる。この値は2:3に近いため、協和音程などと呼ばれる。
上で定義した0から11までの12個の音を全部使えば単純でよいのだが、この中からさらに7個を選ぶ。 なぜ7個なのか、は私にはやはり答えられないが、そういうものである。
ドレミファソラシドは、ドの重複を除くと全部で7個だ、という説明で納得してくれれば嬉しい。
12個の音から7個を選ぶ選び方を、音階と呼ぶ。ざっくり考えると、12C7通りの選び方があるが、実際に使われるのはごく小数である。大きく分けて2つあるようだ。
12段の階段を、7回で登ると決めてしまったのだから、5回は1段飛ばして登らざるを得ない。つまり +12 = (+2) x 5 + (+1) x 2 である。 +1が連続しないように、+2と+1を並べると、並べ方にそんなに自由度はない。
「音階」というのは素晴らしい訳語だと思う。
「要するに、+2を2回やって、+1をやって、+2を3回やって、+1をやって、それで+12になるから、あとはそのリピートでしょ」と思った方:その通りだと思います。
「長音階も短音階も、登り方としては結局同じじゃないか」と思った方:これもその通り。
C Major
{3, 5, 7, 8, 10, 12, 14}
は、12の剰余類としては
{0, 2, 3, 5, 7, 8, 10}
と同値である。
{3, 5, 7, 8, 10, 12, 14}
は、3を中心音として
{0, +2, +2, +1, +2, +2, +2}
だから長音階だが
{0, 2, 3, 5, 7, 8, 10}
は、0を中心音として
{0, +2, +1, +2, +2, +1, +2}
だから短音階である。実際これは、A minor である。
つまり、音の集合としては、C Major = A minor である。
このように、音の集合として一致する調を、平行調と呼ぶ。
ここまでくれば、和音は楽勝である。
調を選んで、その7つの音の中から、1つ飛ばしに3つの音を同時に鳴らせば、それが和音である。たとえば
C Major {3, 5, 7, 8, 10, 12, 14}
には、{3,7,10}という和音がある。関係が、+4,+3 の和音はMajorと呼ばれる。
また、コード名には根音(いちばん下の音)の音名がつく。
つまり和音{3,7,10}は C Major というコードネームを持つ。Cと略記される。
C Majorにおける{7,10,14}は、関係が、+3,+4 であり、minorと呼ばれる。
和音{7,10,14}は E minor である。Emと略記される。
C Majorにおける{14,5,8}~={2,5,8}は、関係が、+3,+3 であり、diminishedと呼ばれる。
和音{2,5,8}は Bdim と略記される。
ということで、C Majorには和音として C/Dm/Em/F/G/Am/Bdimの7つだけ
が存在することがわかる。
これらを順に、Ⅰ/Ⅱ/Ⅲ/Ⅳ/Ⅴ/Ⅵ/Ⅶと記述したりするらしい。
A minor と C Major は平行調なので、存在する7つの和音は当然同一である
・・と思いきや、Wikipediaでイ短調を調べてみると、そうはなっていない。
A minor と C Major の和音が同じでないのは、
A minorとして {0, 2, 3, 5, 7, 8, 10} のほかに、
和声的短音階 {0, 2, 3, 5, 7, 8, 11}
やら、
旋律的短音階 {0, 2, 3, 5, 7, 9, 11}
やらが存在するかららしい。なんでも、
音を高くしていくとき、
主音(この場合は0)の直前の音(この場合は10)から、2上がるのは嫌
なんだそうだ。なので、10の代わりに11を使っちまえ、という発想である。
でも、8と11が+3も違うのは嫌だ、つうことで、
旋律的短音階 +2, +1, +2, +2, +2, +2, (+1)
があるらしい。
ついに階段の登り方が変更されましたいきなりちゃぶ台をひっくり返されて、 「じゃあ、A minor って何なの?」 と叫びたくなる気分である。
ここらで気分を変えて、「なぜ12なのか」を考えてみる。 実はこれは、次のことを認めれば必然の結果なのである。 2つの音の周波数の比が、なるべく簡単な整数の比であることが望ましい もっとも簡単な整数の比は、 1:2 である。 すべての音(正弦波)の集合は、その周波数を考えれば、 正の実数全体の集合 R+ = (0, infinity) と同一視できる。 R+から、基準音440Hzをもとに、..., A2, A3, A4, ... という音を選んだ。 これは周波数だと、等比数列である。公比を2として1オクターブを決めたことが これで説明できた。 次に簡単な整数の比は、1:3 か 2:3 であろう。 2は1の倍なので、どちらで考えても同じことだが、 後々の都合で、2:3で考えることにする。 基準音の周波数をf0として、1オクターブの区間 [ f0, 2 f0 ] の中で両端 f0, 2f0 と (3/2)f0 を含むように、等比数列を取りたい。 両端を含む為には、公比は2のN乗根でなくてはならない。 (3/2)f0 を含むためには 2 ^ (M/N) = (3/2) となるような、自然数 M,N が欲しい。 しかし残念ながら、そのような自然数 M,N は存在しない。 なぜなら、上の式は 2 ^ (M+1) = 3 ^ N となるが、2のべき乗は偶数であり、3のべき乗は奇数だから、 絶対に一致しない。 一般に、比 A:B を実現したいとき、 logを2を底とする対数と決めると、最初の式は (M/N) = log(A/B) = log A - log Bとかけるが、これをみたすような自然数 A,B,M,N は(自明な例を除いて) 存在しないことが証明できる。
ということで、 んじゃ、なるべく 2:3 に近いので我慢する という 人間らしさ を認めるのが音楽理論のおおらかなところである。 (が数学的には、話はややこしくなる。) 公比 2^(1/N) を決めると、(3/2)=1.5 に なるべく近い比を実現する M は M = N log 3 - 1 から自動的に決定する。N=1 から N=14までの範囲で、 N log 3 が、それを四捨五入した整数からどれだけずれているかを 図示すると
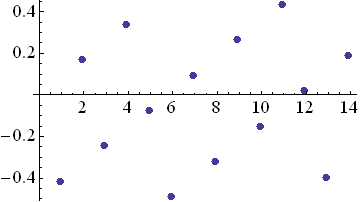
N=12のときに、ずれが非常に小さいことがわかる。 (12 log 3 = 7.01955)
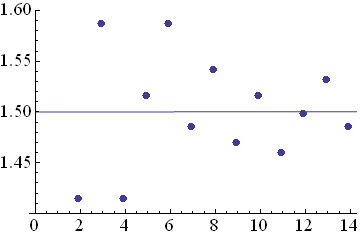
比の値でみると
2^(7/12) = 1.49831
であり、1.5にかなり近い。
余談だが、上の図は Mathematica で
Table[ 2^(Round[N[(i Log[2, 3])]]/i - 1), {i, 14}]
で作成した。
N=5の場合
2^(3/5) = 1.51572
もそれなりに 1.5 に近いので、5平均律というものも考えることができる。
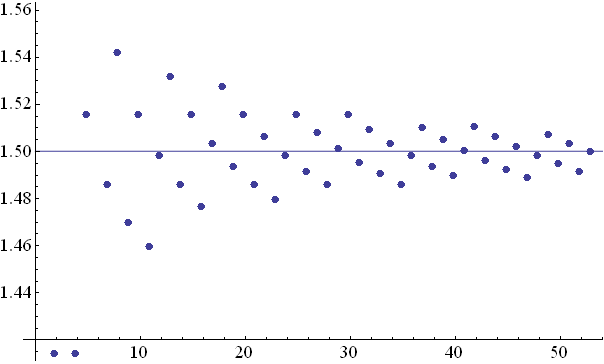
N=12よりもさらに精度良く1.5を実現するためには、 N=24, 36, ... などの12の倍数を除くと、 N=1からN=53の範囲では 2^(17/29) = 1.50129 2^(24/41) = 1.50042 2^(31/53) = 1.49994 と、かなり限られてくる。 N=29にとっても、N=12の場合から大して改善されない (0.00169 → 0.00129) ということで、周波数比 2:3 の精度を、12平均律よりも上げるには、 41平均律 53平均律 くらいしかないのである。 1オクターブを41個やら53個に分けたい とは、普通の人は思わないだろう。 なので、1オクターブを12個に分けるのが標準なのである。
世界標準に立ち向かう精神は重要である。ということで、 [ f0, 3 f0 ] を1オクターブに選んでみることを考える。 この世界は、logで考えると、 上で 2 を底としていたのを、3 を底にすればよいだけである。 そしてこの世界では、周波数比 1:2 を実現するために苦労することになる。 (1:2さえ実現できれば、2:3 は自動的に作れる。) この世界も、通常の世界と同じく、無理数の壁にぶち当たる。 実際のところ、1オクターブを何倍に選ぼうとも、 この問題は解決しない。 よって、いずれにしても 近似値 で我慢するしかない。 ちょっと計算してみると、この世界では 3 ^ (12/19) = 2.00143 を用いて、19平均律が標準となりそうだ。 なお、8平均律 3 ^ (5/8) = 1.98701 65平均律 3 ^ (41/65) = 1.99965 84平均律 3 ^ (53/84) = 2.00005 などが存在しえる。
基準音に対して、 +7 すれば、周波数は 約(3/2)倍 される。
+12 +7 すれば、周波数は 2*(3/2)倍 = 3 倍される。
よって、周波数が3倍3倍になっていくような音列は、
我々の記法では
{0, 19, 38, 57, ...}
となる。
-12 +7 すれば、周波数は (1/2)*(3/2)倍 = (3/4) 倍される。
-5 すれば、周波数は (3/4) 倍されるということは、
+5 すれば周波数は (4/3) 倍されるということである。
+7 +7 -12 すれば、、周波数は (3/2)*(3/2)*(1/2)倍される。
つまり、+2 すれば(全音あげれば)周波数は (9/8)倍になる。
ただしこれらの計算は、すべて近似値であることに注意。
12平均律では、厳密に 2:3 は実現できない。